Solve it...!

 

 

 

 

 

 

 

 

 

 

 

 


























 



 

 

 

 

 

 
Home > Solve it...!

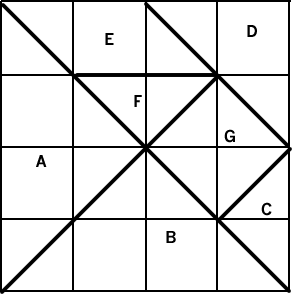
Numeracy problems to solve for Key Stage 1, 2 and 3

Key Stage 1     Solve it...!     Tangrams

Start with a square piece of card (8 cm x 8 cm is a convenient size) and cut it into the seven pieces shown (or you can print this page and cut out the square below).

Now try fitting the pieces together to form the shapes below. Note all seven pieces must be used.

This is an ancient Chinese puzzle which is ageless.

Answer: There are hundreds of possible shapes. To find out more about tangrams go to: http://www.tangrams.ca/

or try the interactive tangram at http://enchantedmind.com/puzzles/tangram/tangram.html

Key Stage 2     Solve it...!     Ever more triangles and squares

Take six drinking straws and cut them in
half to give twelve short straws. Arrange
them to make the two equilateral triangles
shown.

How else could you make two
equilateral triangles using all of the short
straws?

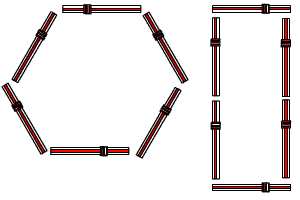
Using all twelve of your short straws in each case show how to make:

a) one equilateral triangle
b) three equilateral triangles
c) four equilateral triangles
d) five equilateral triangles
e) six equilateral triangles
f) eight equilateral triangles

 g) one square
h) two squares
 i) three squares
 j) five squares
k) six squares
l) three squares and eight triangles

What other arrangements can you make using all the straws?

Answer: Here are two different equilateral triangles using all of the short straws:

Key Stage 3     Solve it...!     Carving up the camels

On his deathbed the elderly Arab gathered his three sons
around him and expressed his wish that his 23 prize camels
should be shared among them.

Arab the eldest was to have half of the camels. Azis the second son was to have a third and Abdul the youngest was to have an eight share. Initially pleased with their lot the sons soon realised they had a problem for they couldn't see how they could divide 23 camels into their allotted shares without slaughtering some of them.

In their anguish they turned to their late father's revered
brother for advice. After sleeping on the problem he
lent them one of his own prize camels thus making a total of
24 and suggested they share them out.

Ahab took 12, his half share, Azis then took 8, his third, and Abdul then took 3, his eight share, and then returned his uncle's camel to him with much thanks. Where is the catch?

Answer: The secret is here that:

does not equal 1 but .

When the uncle lent one camel the sons received 12, 8 and 3 camels respectively. But had they not been lent the extra camel they would have received 11.5, 7.66 and 2.875 camels each.

Because the kind uncle lent them the camel every son actually received slightly more than they should have done.

 

Links on this page:
Key Stage 1
Key Stage 2
Key Stage 3

 

 

 


 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


These problems were sourced by North East Lincolnshire's Numeracy Team

Back to the top